Digital Systems:
I have got many emails from students regarding Digital System and Binary Numbers conecpts so this is quick review what is Digital System and Binary Numbers? and what it does.....i think it will help u guys...if u guys really intersted and want to become logical designer Download this book Digital Design (4th Edition) only book that can tech u basics in professional way recommended by many designers...
only book that can tech u basics in professional way recommended by many designers...
I have got many emails from students regarding Digital System and Binary Numbers conecpts so this is quick review what is Digital System and Binary Numbers? and what it does.....i think it will help u guys...if u guys really intersted and want to become logical designer Download this book Digital Design (4th Edition)
Digital systems are used in:
called a bit, has two values: 0 or 1.
Example: The decimal digits a through 9 are represented in digital system with a code
of four bits (e.g. is represented by 0111, 8 is represented by 1000, 9 is represented by
1001).
- Communication
- Business transaction
- Traffic Control
- Medical treatment
- Internet
called a bit, has two values: 0 or 1.
Example: The decimal digits a through 9 are represented in digital system with a code
of four bits (e.g. is represented by 0111, 8 is represented by 1000, 9 is represented by
1001).
Binary Numbers
- Decimal number:
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Example:
The decimal number 245 may be written as
2x102+4x101+5x100
where 2, 4, and 5 are the coefficients.
- Binary Number System:
Example:
(1001)2 its equivalent decimal number is : 1x23+0x22+0x21+1x20 = 8 + 0 + 0 + 1 = 9
where 1, 0, 0, and 1 are the coefficients.
where 1, 0, 0, and 1 are the coefficients.
- Octal number system (Base 8):
The octal number system is said to be of base, or radix, '8' because it uses digits
(00, 01, 02, 03, 04, 05, 06, 07, 10, 11, 12, 13, 14, 15, 16, 17).
(00, 01, 02, 03, 04, 05, 06, 07, 10, 11, 12, 13, 14, 15, 16, 17).
- Hexadecimal number system (Base 16):
It uses 16 digits : (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F). The letter A, B, C, D, E,
and F are used for the digits 10,11, 12, 13, 14, and 15 respectively.
Example:
(124)16 = 1x162 + 2x161 + 4x160= 256 + 32 + 4 = 292
and F are used for the digits 10,11, 12, 13, 14, and 15 respectively.
Example:
(124)16 = 1x162 + 2x161 + 4x160= 256 + 32 + 4 = 292
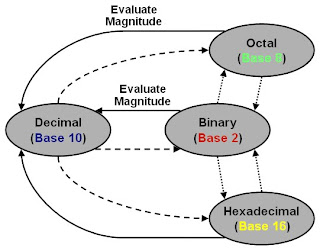
NUMBER BASE CONVERSION
Decimal to Binary conversion
- Divide the number with base '2'.
- Take the remainder 0 or 1 as a coefficient.
- Take the quotient and repeat the division.
Decimal to Octal conversion
Binary to Octal conversion
Binary to Hexadecimal
Octal to Hexadecimal conversion
Complements:
The meaning of complement is something required to make a thing complete. For example, salsa complements tortilla chips, beer complements pizza, an ice cream cone complements a hot summer day, and apple sauce complements pork chops. A key concept to explore is how two things complement each other. For example, when a piece of pizza is removed from a whole pizza the piece complements what is left behind and vice versa. Each of the 4 following complements use the same concept except in different bases and what is considered a complete number in that base.
- 1’s Complement:
- 2’s ComplementFinding the 8 digit 2’s complement of 01101100
- 9’s ComplementThe 9’s complement finds whatever is needed to make an entire set of 9’s. This is shown in the
- 10’s ComplementFinding the 5 digit 10’s complement of 1357
Basic Logic Gate
A logic gate performs a logical operation on one or more logic inputs and produces a single logic output. The logic normally performed is Boolean logic and is most commonly found in digital circuits. Logic gates are primarily implemented electronically using diodes or transistors, but can also be constructed using electromagnetic relays (relay logic), fluidic logic, pneumatic logic, optics, molecules, or even mechanical elements.In electronic logic, a logic level is represented by a voltage or current, (which depends on the type of electronic logic in use). Each logic gate requires power so that it can source and sink currents to achieve the correct output voltage. In a pure logic diagram logic levels and power supply connections do not exist and are not shown, but in a full logic circuit diagram, documenting the implementation of the logic, these are required.
All other types of Boolean logic gates (i.e., AND, OR, NOT, XOR, XNOR) can be created from a suitable network of NAND gates. Similarly all gates can be created from a network of NOR gates. Historically, NAND gates were easier to construct from MOS technology and thus NAND gates served as the first pillar of Boolean logic in electronic computation.
Truth table is a table that describes the behaviour of a logic gate or any combination of logic gates. It lists the value of the output for every possible combination of the inputs and can be used to simplify the number of logic gates and level of nesting in an electronic circuit. In general the truth table does not lead to an efficient implementation; a minimization procedure, using Karnaugh maps, the Quine–McCluskey algorithm or an heuristic algorithm is required for reducing the circuit complexity.
Truth table & Symbols










No comments:
Post a Comment